Explicando probabilidade condicional e o Teorema de Bayes.

Autor

Gilberto Pereira Sassi

Data de Publicação

1 de janeiro de 2024

Neste texto,vamos ver algumas das propriedades das probabilidades começando com probabilidade condicional, e, em seguida, vamos apresentar o Teorema da Probabilidade Total e o Teorema de Bayes.

Probabilidade condicional

Suponha que um camarada descobriu que o resultado do fenômeno aleatório está dentro do evento $B$ , e ele quer saber a probabilidade de um elemento do evento $A$ ser resultado do fenômeno aleatório. Para não ficar repetindo a frase ser resultado do fenômeno aleatório, vamos simplificar: se um elemento do evento $A$ for resultado do fenômeno aleatório, vamos falar que o evento $A$ aconteceu (ou acontece). Neste contexto, a única forma do evento $A$ acontecer é o resultado do fenômeno estar em $A$ e $B$ simultaneamente $(A \cap B)$ , conforme ilustrado na Figura 1.

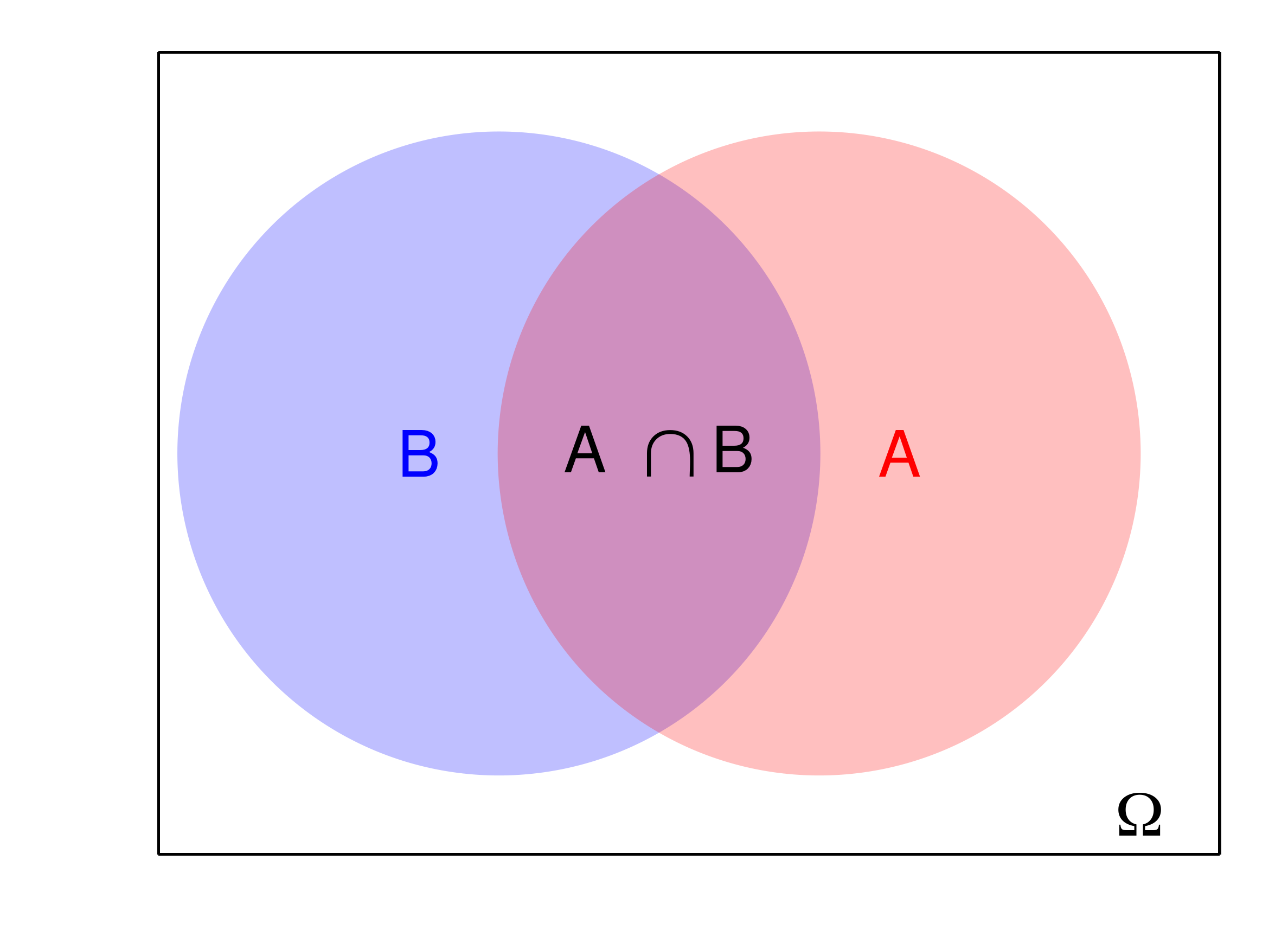
Diagrama de Venn com intersecção entre os eventos $A$ e $B$. A único jeito de A acontecer é se o resultado do fenômeno aleatório estiver dentro de $A \cap B$. — Figura 1: Diagrama de Venn com intersecção entre os eventos A e B. O único jeito de A acontecer é se o resultado do fenômeno aleatório estiver dentro de $A \cap B$ .

Imagine que estamos no contexto em que podemos aplicar o princípio da equiprobabilidade. Considere que o evento $B$ tem $n_{1}$ elementos e que o evento $A \cap B$ tem $n_{2}$ elementos. Além disso, assuma que o espaço amostral tem $N$ elementos. Note que $n_{2} \leq n_{1}$ . Então, temos $n_{1}$ resultados possíveis do fenômeno aleatório (sabemos que $B$ acontece), e a probabilidade de $A$ acontecer (sabendo que $B$ acontece) é dada por $\begin{array}{r} \frac{n_{2}}{n_{1}}, \end{array}$ Note que $\frac{n_{2}}{n_{1}} = \frac{N}{N} \cdot \frac{n_{2}}{n_{1}} = \frac{\frac{n_{2}}{N}}{\frac{n_{1}}{N}}$ . Observe que estamos no princípio da equiprobabilidade, então $P (A \cap B) = \frac{n_{2}}{N}$ e $P (B) = \frac{n_{1}}{N}$ . Consequentemente, concluímos que a probabilidade de $A$ acontecer, se sabemos que $B$ acontece, é dada por $\frac{P (A \cap B)}{P (B)} .$

Chamamos a probabilidade de $A$ acontecer sabendo que $B$ acontece de probabilidade condicional, e em Estatística, resumimos a sentença a probabilidade de $A$ acontecer sabendo que $B$ acontece por probabilidade de $A$ dado $B$ . Usamos a seguinte notação matemática para a probabilidade de $A$ dado $B$ : $P (A ∣ B)$ .

Não precisamos nos restringir ao contexto em que podemos aplicar o princípio da equiprobabilidade, e definimos a probabilidade de $A$ dado $B$ por:

$P (A ∣ B) = \frac{P (A \cap B)}{P (B)}$ , se $P (B) > 0$ ;

Por convenção e conveniência, estabelecemos que $P (A ∣ B) = P (A)$ se $P (B) = 0$ .

Com esta definição de probabilidade condicional, temos a seguinte propriedade chamada de regra do produto:

$P (A \cap B) = P (A ∣ B) P (B)$ ;

$P (A \cap B) = P (B ∣ A) P (A)$ .

Vamos ilustrar as ideias de probabilidade condicional com um exemplo. Imagine cinquenta estudantes distribuídos em duas turmas (Turma $A$ e Turma $B$ ) conforme a tabela abaixo, e queremos escolhê-los por sorteio para formar uma comissão de estudantes.

Gênero	Turma A	Turma B	Total
Masculino	21	16	37
Feminino	5	6	13
Total	26	24	50

Vamos especificar alguns eventos que usaremos em nossa notação matemática. Lembre-se que usamos as letras maiúsculas do alfabeto latino para representar eventos.

$A = estudante da turma A$ ;
$B = estudante da turma B$ ;
$M = estudante se identifica com gênero masculino$ ;
$F = estudante se identifica com gênero feminino$ .

Imagine que queremos escolher por sorteio uma aluna para participar de uma comissão. Neste contexto, sabemos que a pessoa selecionada entre os alunos se identificará com o gênero feminino, e temos $13$ pessoas que se identificam com o gênero feminino. Entre estudantes que se identificam com o gênero feminino, $5$ são da turma $A$ . Então, a probabilidade da aluna ser da turma $A$ é dada por $P (A ∣ F) = \frac{5}{13} = 0, 38.$

Se usarmos a definição de probabilidade condicional, vamos chegar no exato mesmo valor $0, 38$ . De fato, vamos calcular a probabilidade de $A \cap F$ e $F$ usando o princípio da equiprobabilidade, e, depois, usaremos a definição de probabilidade condicional para calcular $P (A ∣ F)$ : $\begin{aligned} P (A \cap F) & = \frac{5}{50} = 0, 1; \\ P (F) & = \frac{13}{50} = 0, 26; \\ P (A ∣ F) & = \frac{P (A \cap F)}{P (F)} = \frac{0, 1}{0, 26} = 0, 38. \end{aligned}$

Teorema da probabilidade total

A partir de agora, vamos fazer algumas mágicas interessantes usando probabilidade condicional. Imagine que o espaço amostral pode ser dividido em algumas partes $C_{1}, \dots, C_{n}$ , conforme ilustrado na Figura 2 onde dividimos o espaço amostral em quatro partes.

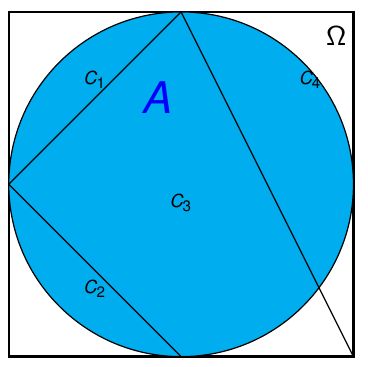
A probabilidade do evento $A$ é a área do quadrado indicada pelo círculo preenchido com a cor azul. Para calcular a probabilidade do evento indicado pelo círculo $A$ , podemos calcular as probabilidades por partes deste círculo

$P (A \cap C_{1})$ ;
$P (A \cap C_{2})$ ;
$P (A \cap C_{3})$ ;
$P (A \cap C_{4})$ ;

e depois somar essas probabilidades para obter a probabilidade do círculo $P (A) = P (A \cap C_{1}) + P (A \cap C_{2}) + P (A \cap C_{3}) + P (A \cap C_{4}),$ e, então, usando a regra do produto em $P (A \cap C_{1})$ , $P (A \cap C_{2})$ , $P (A \cap C_{3})$ e $P (A \cap C_{4})$ temos que $P (A) = P (A ∣ C_{1}) P (C_{1}) + P (A ∣ C_{2}) P (C_{2}) + P (A ∣ C_{3}) P (C_{3}) + P (A ∣ C_{4}) P (C_{4}) .$ Chamamos a coleção dos conjuntos $C_{1}, \dots, C_{4}$ de partição do espaço amostral.

Agora vamos enunciar o Teorema de Probabilidade Total de uma forma geral. Suponha que temos uma participação $C_{1}, \dots, C_{n}$ do espaço amostral e imagine que queremos calcular a probabilidade do evento $A$ . Além disso, imagine que conhecemos as probabilidades:

Probabilidade do evento $C_{1}$ : $P (C_{1})$ ;
Probabilidade do evento $A$ dado $C_{1}$ : $P (A ∣ C_{1})$ ;
Probabilidade do evento $C_{2}$ : $P (C_{2})$ ;
Probabilidade do evento $A$ dado $C_{2}$ : $P (A ∣ C_{2})$ ;
Probabilidade do evento $C_{3}$ : $P (C_{3})$ ;
Probabilidade do evento $A$ dado $C_{3}$ : $P (A ∣ C_{3})$ ;

$⋮$

Probabilidade do evento $C_{n}$ : $P (C_{n})$ ;
Probabilidade do evento $A$ dado $C_{n}$ : $P (A ∣ C_{n})$ ;

Então, podemos calcular a probabilidade do evento $A$ através da seguinte equação $P (A) = P (A ∣ C_{1}) P (C_{1}) + P (A ∣ C_{2}) P (C_{2}) + \dots + P (A ∣ C_{n}) P (C_{n}) .$

Vamos considerar um exemplo simples para ilustrar o uso do Teorema da Probabilidade Total. Imagine que um produtor artesanal de sorvete compra leite de três fazendas: fazenda pequena, fazenda média e fazenda grande. 20% de todo o leite usado por este produtor vem da fazenda pequena, 30% de todo o leite usado por este produtor vem da fazenda média e 50% de todo o leite usado por este produtor vem da fazenda grande. Uma inspenção surpresa da Ministério da Agricultura, Pecuária e Abastecimento (MAPA) descobriu que 10% do leite vendido pela fazenda pequena estava adulterado, 30% do leite vendido pela fazenda média estava adulterado e 20% do leite vendido pela fazenda grande estava adulterado. E agora vem a pergunta: quanto leite adulterado este pequeno produtor artesanal de sorvete comprou destas fazendas?

Primeiro vamos definir alguns eventos: $\begin{aligned} A & = {Galão adulterado}; \\ P & = {Galão produzido pela fazenda pequena}; \\ M & = {Galão produzido pela fazenda média}; \\ G & = {Galão produzido pela fazenda grande}; \end{aligned}$ e sabemos que (usamos as informações do MAPA e do produtor artesanal)

$P (A ∣ P) = 0, 1;$	$P (P) = 0, 2$
$P (A ∣ M) = 0, 3;$	$P (M) = 0, 3$
$P (A ∣ G) = 0, 2;$	$P (G) = 0, 5$

então, usando o Teorema de Probabilidade Total, a proporção (ou probabilidade) de galões adulterados comprados pelo pequeno produtor artesanal de sorvete é dada por $\begin{aligned} P (A) & = P (A ∣ P) P (P) + P (A ∣ M) P (M) + P (A ∣ G) P (G), \\ = 0, 1 \cdot 0, 2 + 0, 3 \cdot 0, 3 + 0, 2 \cdot 0, 5, \\ = 0, 21. \end{aligned}$

Teorema de Bayes

Finalmente, e não menos importante, temos o Teorema de Bayes, que foi descoberto pelo pastor presbiteriano Thomas Bayes. Apesar de matematicamente simples, as implicações e aplicações do Teorema de Bayes são extremamente relevantes para a Probabilidade, Estatística e o conhecimento científico como um todo. O Teorema de Bayes nos permite atualizar a probabilidade ou crença de que um evento $A$ será o resultado de um fenômeno aleatório ao coletarmos ou descobrirmos novas informações ou evidências sobre o fenômeno aleatório.

Reverendo Thomas Bayes. — Figura 3: Thomas Bayes: matemático, filósofo e pastor presbiteriano.

Vamos considerar um exemplo. Imagine que a prevalência de um doença, que denotaremos por $D_{1}$ , no Brasil é $20$ . Ou seja, sem examinar um paciente, um médico estima que este paciente tem a doencça $D_{1}$ com probabilidade $0, 2$ .

Na consulta médica, o paciente descreveu o sintoma $S$ . Da literatura especilizada em medicina, o médico sabe que este sintoma está presente em apenas três doenças: $D_{1}$ , $D_{2}$ e $D_{3}$ . Além disso, o médico sabe que

a probabilidade de um paciente com a doença $D_{1}$ apresentar o sintoma $S$ é $20$ , ou seja, $P (S ∣ D_{1}) = 0, 2$ ;
a probabilidade de um paciente com a doença $D_{2}$ apresentar o sintoma $S$ é $40$ , ou seja, $P (S ∣ D_{2}) = 0, 4$ ;
a probabilidade de um paciente com a doença $D_{3}$ apresentar o sintoma $S$ é $15$ , ou seja, $P (S ∣ D_{3}) = 0, 15$ .

No website do Ministério da Saúde, o médico verificou que a prevalência das doenças $D_{2}$ e $D_{3}$ no Brasil são: $P (D_{2}) = 0, 4$ e $P (D_{3}) = 0, 15$ .

Agora vem a pergunta mais importante: após o médico descobrir que o paciente tem o sintoma $S$ , qual é a probabilidade do paciente ter a doença $D_{1}$ ? Lembre que antes da consulta, o médico diria que a probabilidade deste paciente ter a doença $D_{1}$ é $20$ . Ou seja, queremos calcular a seguinte probabilidade $\begin{array}{r} P (D_{1} ∣ S), \end{array}$ usando a definição de probabilidade condicional e a regra do produto temos que $\begin{aligned} P (D_{1} ∣ S) & = \frac{P (D_{1} \cap S)}{P (S)}, \\ = \frac{P (D_{1}) P (S ∣ D_{1})}{P (S)}, \end{aligned}$ e para calcular $P (S)$ usamos o Teorema da Probabilidade Total $\begin{aligned} P (D_{1} ∣ S) & = \frac{P (D_{1}) P (S ∣ D_{1})}{P (S)}, \\ = \frac{P (D_{1}) P (S ∣ D_{1})}{P (D_{1}) P (S ∣ D_{1}) + P (D_{2}) P (S ∣ D_{2}) + P (D_{3}) P (S ∣ D_{3})}, \\ = \frac{0, 2 \cdot 0, 2}{0, 2 \cdot 0, 2 + 0, 4 \cdot 0, 4 + 0, 4 \cdot 0, 15}, \\ \approx 0, 02 \end{aligned}$

Ou seja, ao descobrir que o paciente tem o sintoma $S$ , o médico ~~mudou~~ atualizou a probabilidade do paciente ter a doença $D_{1}$ de $20$ para $2$ .

Agora vamos enunciar o Teorema de Bayes de uma forma geral. Suponha que temos uma participação $C_{1}, \dots, C_{n}$ do espaço amostral e considere o evento de interesse $A$ . Além disso, imagine que conhecemos as probabilidades:

probabilidade do evento $C_{1}$ : $P (C_{1})$ ;
probabilidade do evento $A$ dado $C_{1}$ : $P (A ∣ C_{1})$ ;
probabilidade do evento $C_{2}$ : $P (C_{2})$ ;
probabilidade do evento $A$ dado $C_{2}$ : $P (A ∣ C_{2})$ ;
probabilidade do evento $C_{3}$ : $P (C_{3})$ ;
probabilidade do evento $A$ dado $C_{3}$ : $P (A ∣ C_{3})$ ; $⋮$
probabilidade do evento $C_{n}$ : $P (C_{n})$ ;
probabilidade do evento $A$ dado $C_{n}$ : $P (A ∣ C_{n})$ ;

Então, as probabilidades dos eventos $C_{i}, i = 1, \dots, n$ acontecerem dado que sabemos ou observamos o evento $A$ é dada por $\begin{aligned} P (C_{1} ∣ A) & = \frac{P (C_{1}) P (A ∣ C_{1})}{P (C_{1}) P (A ∣ C_{1}) + \dots + P (C_{n}) P (A ∣ C_{n})}, \\ P (C_{2} ∣ A) & = \frac{P (C_{2}) P (A ∣ C_{2})}{P (C_{1}) P (A ∣ C_{1}) + \dots + P (C_{n}) P (A ∣ C_{n})}, \\ ⋮ \\ P (C_{n} ∣ A) & = \frac{P (C_{n}) P (A ∣ C_{n})}{P (C_{1}) P (A ∣ C_{1}) + \dots + P (C_{n} 1) P (A ∣ C_{n})} . \end{aligned}$

Vamos fazer mais um exemplo para ilustração. Imagine que uma planta industrial tem três linhas de produção, $L_{1}, L_{2}, L_{3}$ , que produzem lotes de um mesmo equipamento eletrônico. Um lote é considerado inadequado para venda se mais de $10$ dos equipamentos eletrônicos deste lote forem defeituosos. Considere os seguintes eventos

$L_{1} = lote vem da linha de produção L_{1}$
$L_{2} = lote vem da linha de produção L_{2}$
$L_{3} = lote vem da linha de produção L_{3}$
$D = mais de 10 % equipamentos do lote são defeituosos$

Os engenheiros que construíram estas três linhas afirmam que:

a probabilidade da linha de produção $L_{1}$ produzir um lote com mais de $10$ dos equipamentos defeituosos é $35$ , ou seja, $P (D ∣ L_{1}) = 0, 35$ ;
a probabilidade da linha de produção $L_{2}$ produzir um lote com mais de $10$ dos equipamentos defeituosos é $40$ , ou seja, $P (D ∣ L_{2}) = 0, 4$ ;
a probabilidade da linha de produção $L_{3}$ produzir um lote com mais de $10$ dos equipamentos defeituosos é $32, 5$ , ou seja, $P (D ∣ L_{3}) = 0, 325$ ;
$50$ dos lotes desta planta industrial são produzidos pela linha de produção $L_{1}$ , ou seja, $P (L_{1}) = 0, 5$ ;
$30$ dos lotes desta planta industrial são produzidos pela linha de produção $L_{2}$ , ou seja, $P (L_{2}) = 0, 3$ ;
$20$ dos lotes desta planta industrial são produzidos pela linha de produção $L_{3}$ , ou seja, $P (L_{3}) = 0, 2$ .

A equipe do controle de qualidade identificou um lote inadequado, e os engenheiros da planta industrial precisam fazer ajustes nas linhas de produção. A melhor estratégia é começar as análises e ajustes na linha de produção com a maior probabilidade de te ter produzido o lote inadequado. Então, vamos usar o Teorema de Bayes para calcular $P (L_{1} ∣ D), P (L_{2} ∣ D)$ e $P (L_{3} ∣ D)$ :

$\begin{aligned} P (L_{1} ∣ D) & = \frac{P (L_{1}) P (D ∣ L_{1})}{P (D)} \\ = \frac{P (L_{1}) P (D ∣ L_{1})}{P (L_{1}) P (D ∣ L_{1}) + P (L_{1}) P (D ∣ L_{1}) + P (L_{3}) P (D ∣ L_{3})} \\ = \frac{0, 35 \cdot 0, 5}{0, 35 \cdot 0, 5 + 0, 4 \cdot 0, 3 + 0, 2 \cdot 0, 325} \\ = 0, 49 \\ P (L_{2} ∣ D) & = \frac{P (L_{2}) P (D ∣ L_{2})}{P (D)} \\ = \frac{P (L_{2}) P (D ∣ L_{2})}{P (L_{1}) P (D ∣ L_{1}) + P (L_{1}) P (D ∣ L_{1}) + P (L_{3}) P (D ∣ L_{3})} \\ = \frac{0, 4 \cdot 0, 3}{0, 35 \cdot 0, 5 + 0, 4 \cdot 0, 3 + 0, 2 \cdot 0, 325} \\ = 0, 33 \\ P (L_{3} ∣ D) & = \frac{P (L_{3}) P (D ∣ L_{3})}{P (D)} \\ = \frac{P (L_{3}) P (D ∣ L_{3})}{P (L_{1}) P (D ∣ L_{1}) + P (L_{1}) P (D ∣ L_{1}) + P (L_{3}) P (D ∣ L_{3})} \\ = \frac{0, 2 \cdot 0, 325}{0, 35 \cdot 0, 5 + 0, 4 \cdot 0, 3 + 0, 2 \cdot 0, 325} \\ = 0, 18 \end{aligned}$

Ou seja, a linha de produção com maior probabilidade de ter produzido o lote inaquedo é a linha de produção $L_{1}$ , $P (L_{1} ∣ D) = 0, 49$ , e os engenheiros deveriam começar a análise nesta linha de produção.